接触角計/ぬれ性評価装置でできること
接触角とぬれ面積
接触角と
ぬれ方
θ/2法から分かるように、接触角は固体試料に対する液滴の「ぬれ幅」と「液滴高さ」 を使い、三角関数によって求められる数値です。
つまり、液量が同じ場合、ぬれ幅が広くなるほど、液滴高さが低くなるほど、求められる接触角は低くなり、ぬれが良いと評価されます。
これは、ぬれの面積とぬれ性の関係を示していることになります。
つまり、液量が同じ場合、ぬれ幅が広くなるほど、液滴高さが低くなるほど、求められる接触角は低くなり、ぬれが良いと評価されます。
これは、ぬれの面積とぬれ性の関係を示していることになります。

ぬれ面積
接触角の測定では、数値がばらつくことがあるというのが、常識のように言われています。
ばらつくのはぬれ方の違いがあるからで、そうしたぬれ方の違いは上面観測によって明らかになります。
同じ液量でどれだけ「ぬれ広がる」という評価指標となるのが、ぬれ面積です。
界面張力と表面張力
界面張力
界面張力」と聞いてもぴんと来ない人も、「表面張力」と聞くと、すぐにイメージできると思います。
普段「表面張力」と呼んでいるのは、空気中で液体と境界面に働く力のことで、「気-液界面張力」のことです。
液体の界面張力(表面張力)を測定する方法はいくつか存在します。
それぞれにメリットとデメリットがありますが、その中で当社が採用しているのはペンダントドロップ法です。
普段「表面張力」と呼んでいるのは、空気中で液体と境界面に働く力のことで、「気-液界面張力」のことです。
液体の界面張力(表面張力)を測定する方法はいくつか存在します。
それぞれにメリットとデメリットがありますが、その中で当社が採用しているのはペンダントドロップ法です。

接触角計と同一の機器を用いて測定できるため、接触角も測る必要がある場合、あるいは将来測る可能性がある場合などでも、導入コストと設置面積を抑えることができます。
表面張力と表面自由エネルギー
同じ意味
力とエネルギーなので厳密には異なるのですが、「表面張力」と「表面自由エネルギー」は同じと言えます。
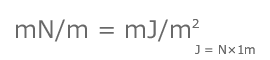
固体の
エネルギー
液体の場合は直接的に表面張力(界面張力、表面自由エネルギー)を測定できますが、同様の方法で固体の表面張力を測定することはできません。
そこで間接的に求めるための方法が、表面自由エネルギーの計算です多くの場合求める対象が固体であるため、表面自由エネルギーというと固体という印象が強いようです。
そこで間接的に求めるための方法が、表面自由エネルギーの計算です多くの場合求める対象が固体であるため、表面自由エネルギーというと固体という印象が強いようです。
理論
固体の表面自由エネルギーを求める理論式は、複数存在します。つまり、確立されていない理論なのです。
それぞれの理論には、既知とする液体の表面自由エネルギーを構成する成分の考え方と割合、そして理論式の立て方に違いがあります。
求め方は、表面自由エネルギーの各成分値が既知である液体(プローブ液体)を用いて接触角を求め、その値を各理論が提唱する式に代入し、対象となる固体の各成分の表面自由エネルギーを求めます。
それぞれの理論には、既知とする液体の表面自由エネルギーを構成する成分の考え方と割合、そして理論式の立て方に違いがあります。
求め方は、表面自由エネルギーの各成分値が既知である液体(プローブ液体)を用いて接触角を求め、その値を各理論が提唱する式に代入し、対象となる固体の各成分の表面自由エネルギーを求めます。

当然のことながら、理論式を変えると計算結果は異なります。
いずれの場合も、計算に用いるのが実測値である接触角なのですが、前ページで述べたように、接触角を求める際には球の一部であるという仮定があり、また測定値はばらつきが生じることもあるため、そうした誤差要因を加味した上で固体の表面自由エネルギー計算結果を取り扱う必要があります。
そうした不確実な理論では役に立たないのかというと、そうでもありません。未知の固体表面が持つ表面自由エネルギーを求める必要性から、指標として用いられています。定理のように鵜呑みにして使うことはできませんが、それぞれの理論の特徴と実験の背景を理解して使う上では、何の手がかりもないままに進むよりは遙かにましであると言えます。
ただし、どの理論に準拠するか、また求められた結果をどのように解釈して扱うかは解析者自身にゆだねられることになります。
