接触角とは何か?
接触角とは、ぬれ性評価における指標のひとつです。
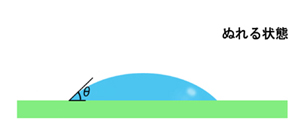
ある固体の上に液体を落としたときにできる液滴の形(液の高さと幅)の程度を数値化したものです。
具体的には、固体上面に付着した液を横から観察し、固体表面を基準に液滴の端点における液滴輪郭の接線との角度を測定します。
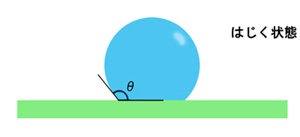
ぬれやすい場合はひらべったく(接触角は低く)なり、ぬれにくい場合は球に近く(接触角は高く)なります。
ある固体の上に液体を落としたときにできる液滴の形(液の高さと幅)の程度を数値化したものです。
具体的には、固体上面に付着した液を横から観察し、固体表面を基準に液滴の端点における液滴輪郭の接線との角度を測定します。
ぬれやすい場合はひらべったく(接触角は低く)なり、ぬれにくい場合は球に近く(接触角は高く)なります。
接触角で何を評価するか
接触角は、固体と液体の相性、つまりぬれ性を評価する指標です。
ほんの一例ですが、下記の様な目的で使われています。
ほんの一例ですが、下記の様な目的で使われています。
- インクの評価
- 液体の品質評価
- 洗浄評価
- コーティング液の評価
- コーティング処理面の性能評価
- など...
接触角の測定方法
接触角は、「液が接触した固体面と液の端点とのなす角度」となるため、一般的には固体試料に付着させた液体試料を横から観測した映像を元に、接触角を測定します。
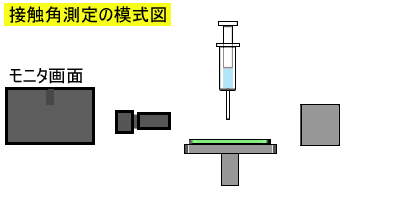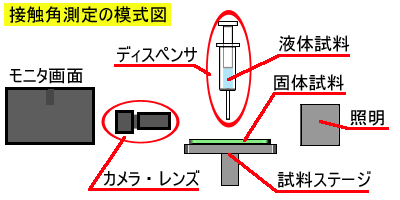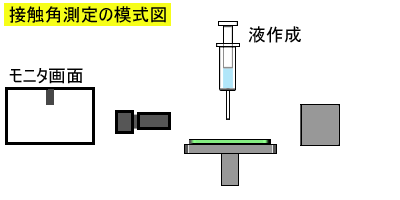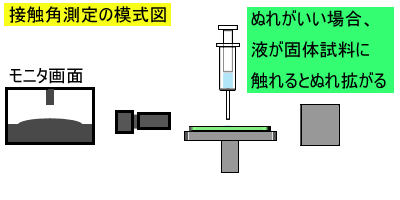
下に示した模式図のように、照明に対向した位置にカメラを設置し、視野内で固体試料に液を付着させて観測することになります。
こうした測定器を『接触角計』といいます。
下に示した模式図のように、照明に対向した位置にカメラを設置し、視野内で固体試料に液を付着させて観測することになります。
こうした測定器を『接触角計』といいます。
ぬれやすい場合
針の先に液を作成し、固体試料を近づけます。
ぬれやすい場合は、固体試料が液に触れると、液は固体試料に引き寄せられてぬれ拡がります。
液体の種別にかかわらず感覚的な意味合いで『親水系』と言われることもあります。
ぬれやすい場合は、固体試料が液に触れると、液は固体試料に引き寄せられてぬれ拡がります。
液体の種別にかかわらず感覚的な意味合いで『親水系』と言われることもあります。

ぬれにくい場合
針の先に液を作成し、固体試料を近づけます。
ぬれにくい場合は、固体試料が液に触れても液は固体試料に引き寄せられにくく液が針から離れないため、ステージを下げます。
液体の種別にかかわらず感覚的な意味合いで『撥水系』『撥油系』と言われることもあります。
ぬれにくい場合は、固体試料が液に触れても液は固体試料に引き寄せられにくく液が針から離れないため、ステージを下げます。
液体の種別にかかわらず感覚的な意味合いで『撥水系』『撥油系』と言われることもあります。

Youngの式
ぬれ拡がりが平衡状態に達した時、固体と液体の表面張力の釣り合いの関係を示した式が「Youngの式」となります。
ぬれ拡がっている途中ではなく、ぬれ拡がりの変化が止まった状態で成立する式です。
そのため、表面自由エネルギーの計算に用いる接触角とは、この平衡状態における接触角となります。
ぬれ拡がっている途中ではなく、ぬれ拡がりの変化が止まった状態で成立する式です。
そのため、表面自由エネルギーの計算に用いる接触角とは、この平衡状態における接触角となります。
<<Youngの式>>
\[
\gamma _S = \gamma _L × \cos \theta + \gamma _{SL}
\]
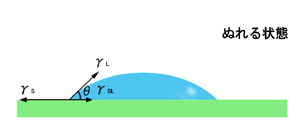
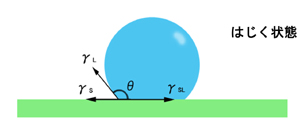
\begin{align}
\gamma _{S } & \text{:固体の表面張力}(\gamma _{SG}) \\
\gamma _{L } & \text{:液体の表面張力}(\gamma _{LG}) \\
\gamma _{SL} & \text{:固体と液体の界面張力}
\end{align}
多くの場合空気は無視されますのでこのように表記されますが、厳密には雰囲気となる気体の影響を加味して、
固体の表面張力 => 固体と気体の界面張力
液体の表面張力 => 液体と気体の界面張力
と考えるのが正しいことになります。
固体の表面張力 => 固体と気体の界面張力
液体の表面張力 => 液体と気体の界面張力
と考えるのが正しいことになります。
θ/2 法とは
最も知られた計算方法が、θ/2 法です。
接触角を直接測定する接触角計で昔から使われてきた方法です。
液滴の輪郭が真円の一部だと仮定すれば、下図の様に固体表面と”接線A”がなす角度θは、液のぬれ幅と高さの関係から明らかとなる関係式、 \[ \tan \frac{\theta}{2} = \frac{h}{r} \] を解けばいいと分かります。
接触角を直接測定する接触角計で昔から使われてきた方法です。
液滴の輪郭が真円の一部だと仮定すれば、下図の様に固体表面と”接線A”がなす角度θは、液のぬれ幅と高さの関係から明らかとなる関係式、 \[ \tan \frac{\theta}{2} = \frac{h}{r} \] を解けばいいと分かります。

\begin{align}
\tan \frac{\theta}{2} & = \frac{h}{r} & \text{より、}\\
\theta & = 2 × arctan \frac{h}{r} & \text{となります。}\\
\\
r \hspace{20px} \text{:} & \hspace{20px} \text{液滴の接触半径}\\
h \hspace{20px} \text{:} & \hspace{20px} \text{液滴の高さ}\\
\end{align}
前提として、横から見た液滴の輪郭が真円の一部をなしている、と考えます。
そのため、左右で接触角が異なる場合や、液滴の自重によるつぶれの影響がある場合には、誤差を含むことになります。
この方法は、最も簡易的な真円フィッティングとも言えます(任意の3点が定まれば円が定まるため)。
そのため、左右で接触角が異なる場合や、液滴の自重によるつぶれの影響がある場合には、誤差を含むことになります。
この方法は、最も簡易的な真円フィッティングとも言えます(任意の3点が定まれば円が定まるため)。
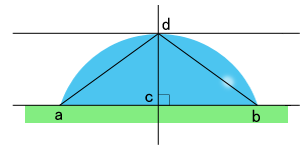
実際には、画像処理において左端点a,右端点bを検出し、線分abの中点cを求め、中点cを通る線分abの垂線と輪郭点との交点dを検出することで、前述のrとhを求めて接触角を算出します。
コンピュータの演算能力が向上した現在においては、輪郭点検出して近似円を求めて演算するカーブフィッティングは標準で実装されています。
カーブフィッティングでは、検出した輪郭点に演算で求めた曲線がどの程度フィットしているかに、注意する必要があります。
コンピュータの演算能力が向上した現在においては、輪郭点検出して近似円を求めて演算するカーブフィッティングは標準で実装されています。
カーブフィッティングでは、検出した輪郭点に演算で求めた曲線がどの程度フィットしているかに、注意する必要があります。
接触角測定において、留意すべき点
ここまでは、最もシンプルな説明となります。
実際の測定においては、接触角が左右で異なる場合があることに、留意しておく必要があります。
このような場合には、左右別々に接触角を測定します。
実際の測定においては、接触角が左右で異なる場合があることに、留意しておく必要があります。
このような場合には、左右別々に接触角を測定します。

また、液滴の左右で接触角が異なる現象が、接触角測定で数値がばらつく要因となります。
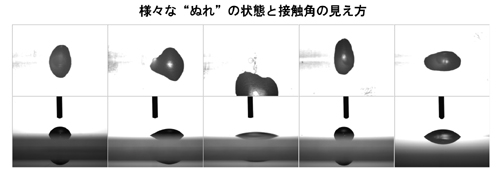
きれいな球の一部としてぬれるのが理想ですが、実際にはいびつな形状にぬれていることがあります。
こうした現象を観察し記録するには、上面観測が必要となります。
接触角を知ろう

